Air compressors work - Compression process
To understand how to save the energy in compressed air system, it is useful to start with theory background of how the air compressors work and how the energy is consumed. As we know from Thermodynamic principle that the compressor work is,
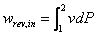
where:
rev = reversible
in = input
Our objective is to minimize the air compressor work that means to approach the reversible process i.e. minimize the friction, and turbulence
Practical way to do this is to make v (specific volume) small by maintaining T (temperature) at low temperature during compression because v a T. In other words, to reduce the work input to a compressor, air should be cooled as it is compressed.
Effect of Cooling
Let's consider the following equations of each process.
Assumptions:
From the above 3 equations, we can plot them in P-v diagram as follows,

where:
Red line represents an isentropic compression process (n=k)
Blue line represents a polytropic compression process (1<n<k)
Green line represents an isothermal compression process (n=1)
Yellow area represents the air compressor work required during compression process of an isothermal process
Because the area from each line to the left is the required air compressor work, we can see that an isothermal process requires loweer amount of energy than polytropic process and isentropic process respectively.
Now we understand that we can save the energy required for compression if we could have some cooling during compression.
Next topic is to see how to save the energy in polytropic compression process which is the case of most air compressors.
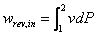
where:
rev = reversible
in = input
Our objective is to minimize the air compressor work that means to approach the reversible process i.e. minimize the friction, and turbulence
Practical way to do this is to make v (specific volume) small by maintaining T (temperature) at low temperature during compression because v a T. In other words, to reduce the work input to a compressor, air should be cooled as it is compressed.
Effect of Cooling
- Isentropic process: No cooling during compression
- Polytropic process: Involve some cooling
- Isothermal process: Involve maximum cooling
Let's consider the following equations of each process.
Assumptions:
- All three processes are executed between the same pressure levels (P1 and P2)
- Reversible process, gas behaves as an ideal gas (Pv = RT)
Isentropic process (Pvk = constant, k = Cp/Cv)
Polytropic process (Pvn = constant)
From the above 3 equations, we can plot them in P-v diagram as follows,

where:
Red line represents an isentropic compression process (n=k)
Blue line represents a polytropic compression process (1<n<k)
Green line represents an isothermal compression process (n=1)
Yellow area represents the air compressor work required during compression process of an isothermal process
Because the area from each line to the left is the required air compressor work, we can see that an isothermal process requires loweer amount of energy than polytropic process and isentropic process respectively.
Now we understand that we can save the energy required for compression if we could have some cooling during compression.
Next topic is to see how to save the energy in polytropic compression process which is the case of most air compressors.


Comments